Inhalt Index DeskTop Bronstein
![]()
![]() Integralrechnung Bestimmte Integrale Grundbegriffe, Regeln und Sätze Berechnung bestimmter Integrale
Integralrechnung Bestimmte Integrale Grundbegriffe, Regeln und Sätze Berechnung bestimmter Integrale
Wenn der Integrand f(x) im Integrationsintervall [a,b] in eine gleichmäßig konvergente Reihe
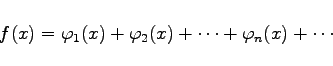 |
(8.52) |
entwickelt werden kann, dann läßt sich das Integral in der Form
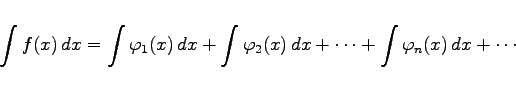 |
(8.53) |
schreiben. Auf diese Weise kann das bestimmte Integral als konvergente numerische Reihe dargestellt werden:
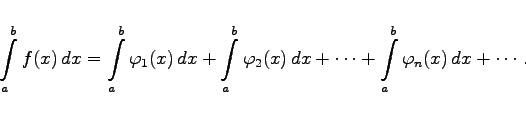 |
(8.54) |
Im Falle leicht zu integrierender Funktionen ![]() , wenn z.B. f(x) in eine Potenzreihe entwickelt werden kann, die im Intervall [a,b] gleichmäßig konvergiert, kann das Integral
, wenn z.B. f(x) in eine Potenzreihe entwickelt werden kann, die im Intervall [a,b] gleichmäßig konvergiert, kann das Integral 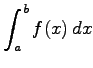 mit beliebiger Genauigkeit berechnet werden.
mit beliebiger Genauigkeit berechnet werden.
| Beispiel |
|
Das Integral |