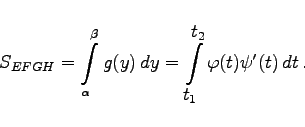Flächeninhalt eines seitlich zwischen den Punkten
G und
H krummlinig begrenzten Trapezes: Der Flächeninhalt eines seitlich zwischen den Punkten
G und
H krummlinig begrenzten Trapezes (s. rechte Abbildung) bei explizit (
x=g(y) und
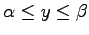
) bzw. in Parameterform (

) gegebener Kurvengleichung:
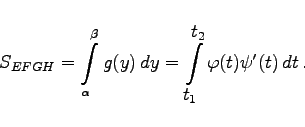 |
(8.59b) |
![]()
![]() Integralrechnung Bestimmte Integrale Anwendungen bestimmter Integrale Anwendungen in der Geometrie
Integralrechnung Bestimmte Integrale Anwendungen bestimmter Integrale Anwendungen in der Geometrie