Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Partielle Differentialgleichungen Schrödinger-Gleichung Statistische Interpretation der Wellenfunktion
Differentialgleichungen Partielle Differentialgleichungen Schrödinger-Gleichung Statistische Interpretation der Wellenfunktion
Eine physikalische Größe (Ort, Impuls, Drehimpuls, Energie), die durch eine geeignete Meßanordnung bestimmt werden kann, bezeichnet man als Observable. In der Quantenmechanik wird jede Observable A durch einen linearen, hermiteschen Operator ![]() mit
mit ![]() repräsentiert, der auf die Wellenfunktion wirkt. Dabei wird beim Übergang zum Operator der Quantenmechanik die Struktur der klassischen Größe übernommen.
repräsentiert, der auf die Wellenfunktion wirkt. Dabei wird beim Übergang zum Operator der Quantenmechanik die Struktur der klassischen Größe übernommen.
| Beispiel Drehimpulsoperator | ||||||||
|
Für den Operator
|
Einer Observablen kann ein bestimmter numerischer Wert im allgemeinen nicht durch die Angabe der Wellenfunktion sondern erst als Ergebnis einer Messung zugeschrieben werden. Die einzig möglichen Meßwerte von A sind dabei die reellen Eigenwerte ai von ![]() ; die zugehörigen Eigenfunktionen
; die zugehörigen Eigenfunktionen ![]() bilden ein vollständiges Orthonormalsystem:
bilden ein vollständiges Orthonormalsystem:
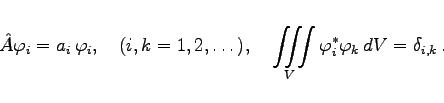 |
(9.123) |
Befindet sich das System in einem beliebigen, allgemeinen Zustand ![]() , dann ist der Ausgang eines individuellen Experiments, d.h. das Auftreten eines bestimmten Meßwertes ai in einer Einzelmessung nicht vorhersagbar. Denkt man sich aber die Messung an
, dann ist der Ausgang eines individuellen Experiments, d.h. das Auftreten eines bestimmten Meßwertes ai in einer Einzelmessung nicht vorhersagbar. Denkt man sich aber die Messung an ![]() identischen Systemen im gleichen Zustand
identischen Systemen im gleichen Zustand ![]() ausgeführt, dann tritt unter den Meßergebnisse jeder mögliche Meßwert ai mit einer Häufigkeit Ni auf. Man kann dann eine Wahrscheinlichkeit Wi dafür angeben, in einer Einzelmessung den Meßwert ai zu finden:
ausgeführt, dann tritt unter den Meßergebnisse jeder mögliche Meßwert ai mit einer Häufigkeit Ni auf. Man kann dann eine Wahrscheinlichkeit Wi dafür angeben, in einer Einzelmessung den Meßwert ai zu finden:
 |
(9.124) |
Um diese Wahrscheinlichkeit aus der Wellenfunktion ![]() zu ermitteln, wird
zu ermitteln, wird ![]() nach den Eigenfunktionen
nach den Eigenfunktionen ![]() entwickelt:
entwickelt:
 |
(9.125) |
Der Entwicklungskoeffizient ci ist die Wahrscheinlichkeitsamplitude dafür, im Zustand ![]() das System im Eigenzustand
das System im Eigenzustand ![]() anzutreffen und folglich den Meßwert ai zu erzielen. Das Absolutquadrat von ci liefert dann die Wahrscheinlichkeit Wi für den Meßwert ai:
anzutreffen und folglich den Meßwert ai zu erzielen. Das Absolutquadrat von ci liefert dann die Wahrscheinlichkeit Wi für den Meßwert ai:
 |
(9.126) |
Da bei jeder Messung mit Sicherheit einer der möglichen Meßwerte ai gefunden wird, entspricht die Summe der Wahrscheinlichkeiten Wi der Normierungsbedingung für die Wellenfunktion ![]() .
.
Sind zwei Zustände ![]() eines physikalischen Systems bekannt, dann folgt aus der Linearität der SCHR¨ODINGER-Gleichung, daß die Überlagerung
eines physikalischen Systems bekannt, dann folgt aus der Linearität der SCHR¨ODINGER-Gleichung, daß die Überlagerung
 |
(9.127) |
ebenfalls einen möglichen physikalischen Zustand darstellt. Dieses fundamentale Superpositionsprinzip der Quantenmechanik bedingt, daß bei der Berechnung von Wahrscheinlichkeiten mit der Zustandsfunktion ![]() , etwa
, etwa
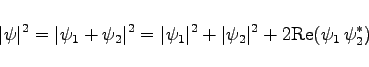 |
(9.128) |
wegen der zugrundliegenden, vorangegangenen Addition von Wahrscheinlichkeitsamplituden neben der Summe der Einzelwahrscheinlichkeiten ![]() ein vorzeichenbehafteter Zusatzterm auftritt, der die überraschenden Interferenzerscheinungen in der Quantenmechanik bewirkt (Welle-Teilchen-Dualismus).
ein vorzeichenbehafteter Zusatzterm auftritt, der die überraschenden Interferenzerscheinungen in der Quantenmechanik bewirkt (Welle-Teilchen-Dualismus).