Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Partielle Differentialgleichungen Nichtlineare partielle Differentialgleichungen: Solitonen, periodische Muster und Chaos Korteweg-de-Vries-Gleichung
Differentialgleichungen Partielle Differentialgleichungen Nichtlineare partielle Differentialgleichungen: Solitonen, periodische Muster und Chaos Korteweg-de-Vries-Gleichung
Die KdV-Gleichung für die Evolutionsfunktion u lautet
Sie hat die Soliton-Lösung
Dieses KdV-Soliton ist durch die zwei dimensionslosen Parameter ![]() und
und ![]() eindeutig bestimmt, und ist in der Abbildung ist v=1 dargestellt. Ein typisch nichtlinearer Effekt besteht darin, daß die Solitongeschwindigkeit v die Amplitude und die Breite des Solitons bestimmt: KdV-Solitonen mit größerer Amplitude und geringerer Breite bewegen sich schneller als solche mit kleinerer Amplitude und größerer Breite. Die Solitonphase
eindeutig bestimmt, und ist in der Abbildung ist v=1 dargestellt. Ein typisch nichtlinearer Effekt besteht darin, daß die Solitongeschwindigkeit v die Amplitude und die Breite des Solitons bestimmt: KdV-Solitonen mit größerer Amplitude und geringerer Breite bewegen sich schneller als solche mit kleinerer Amplitude und größerer Breite. Die Solitonphase ![]() beschreibt die Lage des Maximums des Solitons zur Zeit
beschreibt die Lage des Maximums des Solitons zur Zeit ![]()
Die Gleichung (9.160) besitzt auch N-Solitonenlösungen. Eine solche N-Solitonenlösung läßt sich für ![]() asymptotisch durch lineare Überlagerung von Ein-Solitonlösungen darstellen:
asymptotisch durch lineare Überlagerung von Ein-Solitonlösungen darstellen:
 |
(9.162) |
Dabei ist jede Evolutionsfunktion un(x,t) durch eine Geschwindigkeit vn und eine Phase ![]() gekennzeichnet. Die Anfangsphasen
gekennzeichnet. Die Anfangsphasen ![]() vor der Wechselwirkung oder dem Stoßprozeß unterscheiden sich von den Endphasen nach dem Stoß
vor der Wechselwirkung oder dem Stoßprozeß unterscheiden sich von den Endphasen nach dem Stoß ![]() , während die Geschwindigkeiten
, während die Geschwindigkeiten ![]() keine Änderung erfahren, d.h., es handelt sich um eine elastische Wechselwirkung.
keine Änderung erfahren, d.h., es handelt sich um eine elastische Wechselwirkung.
Für N=2 besitzt (9.160) eine 2-Solitonenlösung. Sie läßt sich für endliche Zeiten nicht durch lineare Überlagerung darstellen und lautet mit  und
und  :
:
Diese Gleichung (9.163) beschreibt asymptotisch zwei für ![]() nicht wechselwirkende Solitonen mit den Geschwindigkeiten v1=4k12 und
nicht wechselwirkende Solitonen mit den Geschwindigkeiten v1=4k12 und ![]() , die nach einem Wechselwirkungsprozeß für
, die nach einem Wechselwirkungsprozeß für ![]() wieder asymptotisch in zwei nichtwechselwirkende Solitonen mit denselben Geschwindigkeiten übergehen.
wieder asymptotisch in zwei nichtwechselwirkende Solitonen mit denselben Geschwindigkeiten übergehen.
Die nichtlineare Evolutionsgleichung

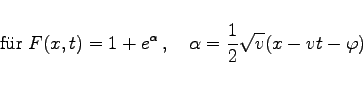 |
(9.164b) |
eine Solitonlösung und
eine 2-Solitonenlösung. Mit 2wx=u ergibt sich aus (9.164a) die KdV-Gleichung (9.160). Die Gleichung (9.163) und der sich mit (9.164c) ergebende Ausdruck für w sind Beispiele für eine nichtlineare Superposition. Ersetzt man in (9.160) den Term +6uux durch -6uux, so muß die rechte Seite von (9.161) mit (-1) multipliziert werden. Man spricht dann auch von einem Antisoliton.