Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Gewöhnliche Differentialgleichungen Differentialgleichungen 1. Ordnung Implizite Differentialgleichungen
Differentialgleichungen Gewöhnliche Differentialgleichungen Differentialgleichungen 1. Ordnung Implizite Differentialgleichungen
CLAIRAUTsche Differentialgleichung heißt der Spezialfall der LAGRANGEschen Differentialgleichung, der sich für
 |
(9.16a) |
ergibt, und der stets auf die Form
| y=y'x+f(y') | (9.16b) |
gebracht werden kann. Die allgemeine Lösung lautet
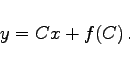 |
(9.16c) |
Neben der allgemeinen Lösung besitzt die CLAIRAUTsche Differentialgleichung ein singuläres Integral, das man durch Elimination der Konstanten C aus den Gleichungen
| y=Cx+f(C) | (9.16d) |
 |
(9.16e) |
erhält, wobei die zweite Gleichung aus der ersten durch Differentiation nach C gewonnen wird. Die geometrische Bedeutung der singulären Lösung besteht darin, daß sie die Einhüllende der lösenden Geradenschar darstellt (s. Abbildung).
| Beispiel |
|
Es ist die Differentialgleichung y=xy'+y'2 zu lösen. Das allgemeine Integral ist |