Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Gewöhnliche Differentialgleichungen Differentialgleichungen höherer Ordnung und Systeme von Differentialgleichungen Grundlegende Betrachtungen
Differentialgleichungen Gewöhnliche Differentialgleichungen Differentialgleichungen höherer Ordnung und Systeme von Differentialgleichungen Grundlegende Betrachtungen
Jede explizite Differentialgleichung n-ter Ordnung
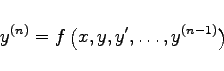 |
(9.22a) |
kann durch Einführung der neuen Variablen
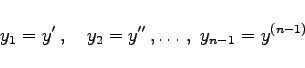 |
(9.22b) |
auf ein System von n Differentialgleichungen 1. Ordnung
zurückgeführt werden.
Das im Vergleich zu (9.22c) allgemeinere System von n Differentialgleichungen
besitzt ein eindeutig bestimmtes Lösungssystem
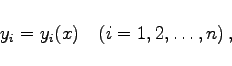 |
(9.23b) |
das in einem Intervall ![]() definiert und stetig ist und für x = x0 die vorgegebenen Anfangswerte
definiert und stetig ist und für x = x0 die vorgegebenen Anfangswerte ![]() annimmt, wenn die Funktionen
annimmt, wenn die Funktionen ![]() bezüglich aller Variablen stetig sind und die folgende LIPSCHITZ-Bedingung erfüllen.
bezüglich aller Variablen stetig sind und die folgende LIPSCHITZ-Bedingung erfüllen.
Die Funktionen fi müssen für die Werte ![]() und
und ![]() , die in einem gewissen Intervall in der Umgebung der gegebenen Anfangswerte liegen, den Ungleichungen
, die in einem gewissen Intervall in der Umgebung der gegebenen Anfangswerte liegen, den Ungleichungen
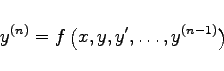 |
(9.25) |
eine eindeutige Lösung besitzt, die die Anfangsbedingungen ![]() für x = x0 erfüllt und zusammen mit ihren Ableitungen bis einschließlich der (n - 1)-ten Ordnung stetig ist.
für x = x0 erfüllt und zusammen mit ihren Ableitungen bis einschließlich der (n - 1)-ten Ordnung stetig ist.