Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Gewöhnliche Differentialgleichungen Randwertprobleme Problemstellung
Differentialgleichungen Gewöhnliche Differentialgleichungen Randwertprobleme Problemstellung
Selbstadjungierte Differentialgleichung wird die folgende wichtige Form der Differentialgleichungen 2. Ordnung genannt:
Als lineare Randbedingungen werden die homogenen Bedingungen
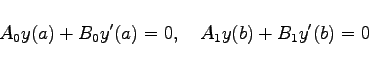 |
(9.73b) |
vorgegeben. Die Funktionen ![]() und f(x) sollen in dem endlichen Intervall
und f(x) sollen in dem endlichen Intervall ![]() stetig sein. Im Falle eines unendlichen Intervalls ändern sich die Ergebnisse ganz wesentlich (s. [9.5]). Außerdem wird verlangt, daß
stetig sein. Im Falle eines unendlichen Intervalls ändern sich die Ergebnisse ganz wesentlich (s. [9.5]). Außerdem wird verlangt, daß ![]() gilt. Die Größe
gilt. Die Größe ![]() , ein Parameter der Differentialgleichung, ist konstant. Für f =0 ergibt sich zum inhomogenen Randwertproblem das zugehörige homogene Randwertproblem.
, ein Parameter der Differentialgleichung, ist konstant. Für f =0 ergibt sich zum inhomogenen Randwertproblem das zugehörige homogene Randwertproblem.
Jede Differentialgleichung 2. Ordnung
 |
(9.73c) |
kann, falls in ![]() ist, durch Multiplikation mit p/A auf die selbstadjungierte Form (9.73a) gebracht werden. Dazu sind die Substitutionen
ist, durch Multiplikation mit p/A auf die selbstadjungierte Form (9.73a) gebracht werden. Dazu sind die Substitutionen
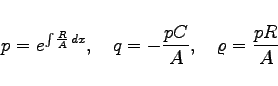 |
(9.73d) |
erforderlich.
Um eine Lösung zu finden, die den inhomogenen Bedingungen
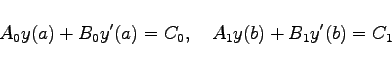 |
(9.73e) |
genügt, geht man auf eine Aufgabe mit homogenen Bedingungen, aber geänderter rechter Seite der Differentialgleichung, zurück, indem man die unbekannte Funktion mit Hilfe der Substitution y =z + u ersetzt. Dabei ist u eine beliebige, zweimal differenzierbare Funktion, die die inhomogenen Randbedingungen erfüllt, während z eine neue unbekannte Funktion ist, die die zugehörigen homogenen Randbedingungen erfüllt.