Wenn in (
9.73a) die Koeffizienten
p(x) und
q(x) durch
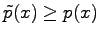
und
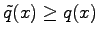
ersetzt werden, dann werden die Eigenwerte nicht kleiner, sondern es gilt

, wobei
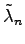
und
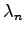
die
n-ten Eigenwerte der geänderten bzw. ungeänderten Gleichung sind. Wenn jedoch der Koeffizient

durch
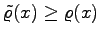
ersetzt wird, dann werden die Eigenwerte nicht größer, sondern es gilt
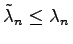
. Der
n-te Eigenwert hängt hierbei stetig von den Koeffizienten der Gleichung ab, d.h., hinreichend kleinen Änderungen der Koeffizienten entsprechen beliebig kleine Änderungen des
n-ten Eigenwertes.
![]()
![]() Differentialgleichungen Gewöhnliche Differentialgleichungen Randwertprobleme
Differentialgleichungen Gewöhnliche Differentialgleichungen Randwertprobleme
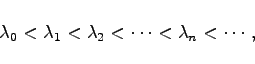

![]() das Gewicht der Orthogonalität genannt wird.
das Gewicht der Orthogonalität genannt wird.