Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Partielle Differentialgleichungen Partielle Differentialgleichungen 1. Ordnung Nichtlineare partielle Differentialgleichungen 1. Ordnung
Differentialgleichungen Partielle Differentialgleichungen Partielle Differentialgleichungen 1. Ordnung Nichtlineare partielle Differentialgleichungen 1. Ordnung
Gleichungen dieser Art haben die Gestalt
wobei die ![]() gegebene Funktionen der Variablen
gegebene Funktionen der Variablen ![]() sind. Man spricht von einer vollständig integrierbaren Differentialgleichung, wenn sich eine eindeutige Beziehung zwischen den
sind. Man spricht von einer vollständig integrierbaren Differentialgleichung, wenn sich eine eindeutige Beziehung zwischen den ![]() angeben läßt, die einen frei wählbaren konstanten Faktor enthält, und die auf die Gleichung (9.87a) führt. Dann existiert eine eindeutige Lösung
angeben läßt, die einen frei wählbaren konstanten Faktor enthält, und die auf die Gleichung (9.87a) führt. Dann existiert eine eindeutige Lösung ![]() von (9.87a), die für die Anfangswerte
von (9.87a), die für die Anfangswerte ![]() der unabhängigen Veränderlichen einen vorgegebenen Wert z0 ergibt. Daraus folgt für
der unabhängigen Veränderlichen einen vorgegebenen Wert z0 ergibt. Daraus folgt für ![]() , daß durch jeden Raumpunkt eine und nur eine Integralfläche verläuft.
, daß durch jeden Raumpunkt eine und nur eine Integralfläche verläuft.
Vollständige Integrabilität gibt es für die Differentialgleichung (9.87a) dann und nur dann, wenn die  Beziehungen
Beziehungen
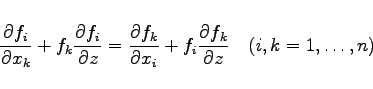 |
(9.87b) |
in allen Variablen ![]() identisch erfüllt sind.
identisch erfüllt sind.
Wenn die Differentialgleichung in der symmetrischen Gestalt
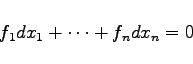 |
(9.87c) |
gegeben ist, dann lautet die Bedingung für die vollständige Integrabilität für alle Kombinationen der Indizes i, j, k
 |
(9.87d) |
Liegt vollständige Integrabilität vor, dann kann die Auflösung der Differentialgleichung (9.87a) auf die Integration einer gewöhnlichen Differentialgleichung mit n-1 Parametern zurückgeführt werden.