Allgemeine Form
Allgemeine Form einer linearen partiellen Differentialgleichung 2. Ordnung mit zwei unabhängigen Variablen x,y und einer unbekannten Funktion u heißt eine Gleichung der Gestalt
 |
(9.88a) |
wobei die Koeffizienten A,B,C,a,b,c und das freie Glied f bekannte Funktionen von x und y sind.
Die Form der Lösung dieser Differentialgleichung hängt vom Vorzeichen der Diskriminante
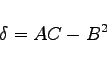 |
(9.88b) |
in einem betrachteten Gebiet ab. Man unterscheidet die folgenden Formen:
-
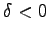
: Hyperbolischer Typ.
-

: Parabolischer Typ.
-
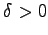
: Elliptischer Typ.
-

ändert sein Vorzeichen: Gemischter Typ.
Eine wichtige Eigenschaft der Diskriminante  besteht darin, daß ihr Vorzeichen invariant ist gegen beliebige Transformationen der unabhängigen Variablen, z.B. bei der Einführung neuer Koordinaten in der x,y-Ebene. Somit ist auch der Typ der Differentialgleichung eine Invariante bezüglich der Wahl der unabhängigen Variablen.
besteht darin, daß ihr Vorzeichen invariant ist gegen beliebige Transformationen der unabhängigen Variablen, z.B. bei der Einführung neuer Koordinaten in der x,y-Ebene. Somit ist auch der Typ der Differentialgleichung eine Invariante bezüglich der Wahl der unabhängigen Variablen.
![]()
![]() Differentialgleichungen Partielle Differentialgleichungen Lineare partielle Differentialgleichungen 2. Ordnung Klassifikation und Eigenschaften der Differentialgleichungen 2. Ordnung mit zwei unabhängigen Veränderlichen
Differentialgleichungen Partielle Differentialgleichungen Lineare partielle Differentialgleichungen 2. Ordnung Klassifikation und Eigenschaften der Differentialgleichungen 2. Ordnung mit zwei unabhängigen Veränderlichen