Zwei Elemente x, y eines HILBERT-Raumes (die Begriffe dieses Abschnitts haben auch in Prä-HILBERT-Räumen bzw. in unitären Räumen Sinn) 
heißen orthogonal (man schreibt dafür 
), wenn 
. Für eine beliebige Teilmenge 
ist die Menge
 |
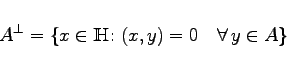(12.114) |
aller Vektoren, die zu jedem Vektor aus A orthogonal sind, ein (abgeschlossener linearer) Teilraum von und heißt Orthogonalraum zu A oder orthogonales Komplement von 
. Man schreibt 
, wenn 
und 
gilt. Besteht A nur aus dem Element 
, dann schreibt man 
.