Inhalt Index DeskTop Bronstein
![]()
![]() Integraltransformationen Fourier-Transformation Eigenschaften der Fourier-Transformation Fourier-Transformation und Umkehrtransformation
Integraltransformationen Fourier-Transformation Eigenschaften der Fourier-Transformation Fourier-Transformation und Umkehrtransformation
In Analogie zur FOURIER-Reihe einer periodischen Funktion erfährt das FOURIER-Integral für eine nichtperiodische Funktion eine einfache physikalische Interpretation.
 |
(15.79a) |
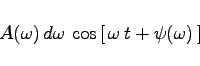 |
(15.79b) |
dargestellt werden.
 |
(15.80) |
wobei die Größe  sowohl die Amplitude als auch die Phase aller Teilvorgänge festlegt.
sowohl die Amplitude als auch die Phase aller Teilvorgänge festlegt.
 |
(15.81a) |
nennt man Spektrum oder Frequenzspektrum der Funktion ![]() , die Größe
, die Größe
 |
(15.81b) |
das Amplitudenspektrum und ![]() bzw.
bzw. ![]() das Phasenspektrum der Funktion
das Phasenspektrum der Funktion ![]() . Zwischen dem Spektrum
. Zwischen dem Spektrum ![]() und den Koeffizienten (15.66b,c) besteht die Beziehung
und den Koeffizienten (15.66b,c) besteht die Beziehung
woraus sich die folgenden Aussagen ergeben:
| Beispiel |
|
Setzt man das Ergebnis (A.2) für den unipolaren Rechteckimpuls in (15.82) ein, dann ergibt sich für die Bildfunktion  |