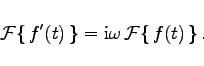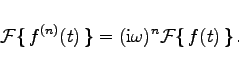- 1. Differentiation im Bildbereich:
- Ist tnf(t) FOURIER-transformierbar, dann gilt
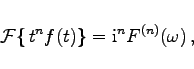 |
(15.88) |
wobei mit  die n-te Ableitung von
die n-te Ableitung von 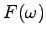 bezeichnet ist.
bezeichnet ist.
- 2. Differentiation im Originalbereich:
-
- a) Erste Ableitung:
- Ist eine Funktion f(t) stetig und absolut integrierbar in
 und strebt sie für
und strebt sie für 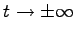 gegen Null und existiert, ausgenommen gewisse Punkte, überall die Ableitung
gegen Null und existiert, ausgenommen gewisse Punkte, überall die Ableitung  , die in
, die in  absolut integrierbar sein muß, dann gilt
absolut integrierbar sein muß, dann gilt
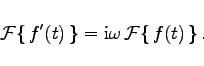 |
(15.89a) |
- b) n-te Ableitung:
- Stellt man in der Verallgemeinerung des Satzes für die 1. Ableitung an alle weiteren Ableitungen bis zur (n-1)-ten f(n-1) die gleichen Anforderungen, dann gilt
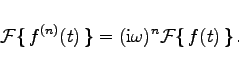 |
(15.89b) |
Diese Differentiationsregeln werden bei der Lösung von Differentialgleichungen angewendet.
![]()
![]() Integraltransformationen Fourier-Transformation Eigenschaften der Fourier-Transformation Rechenregeln zur Fourier-Transformation
Integraltransformationen Fourier-Transformation Eigenschaften der Fourier-Transformation Rechenregeln zur Fourier-Transformation
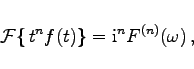
![]() die n-te Ableitung von
die n-te Ableitung von ![]() bezeichnet ist.
bezeichnet ist.