Inhalt Index DeskTop Bronstein
![]()
![]() Integraltransformationen Fourier-Transformation Lösung von Differentialgleichungen mit Hilfe der Fourier-Transformation Partielle Differentialgleichungen
Integraltransformationen Fourier-Transformation Lösung von Differentialgleichungen mit Hilfe der Fourier-Transformation Partielle Differentialgleichungen
Wie die dreidimensionale Wellengleichung (9.111a), so ist auch 15.104a eine partielle Differentialgleichung vom hyperbolischen Typ. Das CAUCHYsche Problem sei durch die Anfangsbedingungen
 |
(15.104b) |
korrekt gestellt.
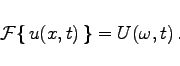 |
(15.105a) |
Daraus ergibt sich:
Die allgemeine Lösung dieser bekannten Differentialgleichung mit konstanten Koeffizienten lautet
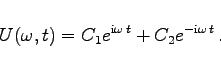 |
(15.106a) |
Mit Hilfe der Anfangsbedingungen
 |
(15.106b) |
lassen sich die Konstanten C1 und C2 bestimmen:
 |
(15.106c) |
Die Lösung ergibt sich zu
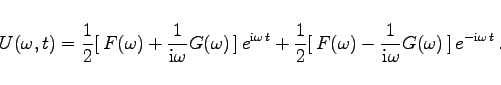 |
(15.106d) |
 |
(15.107a) |
mit Vorteil eingesetzt werden, woraus sich ergibt
 |
(15.107b) |
Die Anwendung der Integrationsregel
 |
(15.107e) |
Die endgültige Lösung im Originalbereich lautet somit
 |
(15.108) |