Inhalt Index DeskTop Bronstein
![]()
![]() Wahrscheinlichkeitsrechnung und Mathematische Statistik Wahrscheinlichkeitsrechnung Zufallsgrößen, Verteilungsfunktionen Verteilungsfunktion
Wahrscheinlichkeitsrechnung und Mathematische Statistik Wahrscheinlichkeitsrechnung Zufallsgrößen, Verteilungsfunktionen Verteilungsfunktion
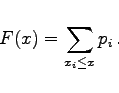 |
(16.45) |
darstellen, dann spricht man von einer stetigen Verteilungsfunktion
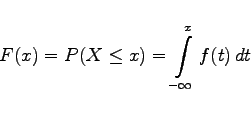 |
(16.47) |
und einer stetigen Zufallsgröße.
Hinweis: Wenn keine Verwechslung mit der oberen Integrationsgrenze möglich ist, wird häufig die Integrationsveränderliche anstelle von t mit x bezeichnet.