Inhalt Index DeskTop Bronstein
![]()
![]() Wahrscheinlichkeitsrechnung und Mathematische Statistik Kombinatorik
Wahrscheinlichkeitsrechnung und Mathematische Statistik Kombinatorik
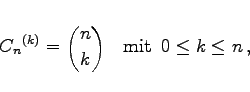 |
(16.4) |
wobei jedes der n Elemente höchstens einmal in einer Kombination auftreten darf. Man spricht deshalb auch von einer Kombination ohne Wiederholung.
| Beispiel |
|
Es gibt |
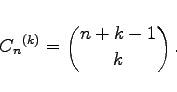 |
(16.5) |
Eine andere Formulierung lautet, daß die Anzahl der Möglichkeiten betrachtet wird, aus n verschiedenen Elementen je k zusammenzustellen, wobei die k Elemente nicht verschieden zu sein brauchen.
| Beispiel |
|
Mit k Würfeln sind |