Inhalt Index DeskTop Bronstein
![]()
![]() Wahrscheinlichkeitsrechnung und Mathematische Statistik Mathematische Statistik Wichtige Prüfverfahren Vertrauensgrenzen für den Mittelwert
Wahrscheinlichkeitsrechnung und Mathematische Statistik Mathematische Statistik Wichtige Prüfverfahren Vertrauensgrenzen für den Mittelwert
Es sei X eine kontinuierliche Zufallsgröße, normalverteilt mit den Parametern ![]() und
und ![]() . Gemäß Abschnitt Verteilung der Stichprobenmittelwerte ist dann
. Gemäß Abschnitt Verteilung der Stichprobenmittelwerte ist dann ![]() ebenfalls eine kontinuierliche Zufallsgröße, normalverteilt mit den Parametern
ebenfalls eine kontinuierliche Zufallsgröße, normalverteilt mit den Parametern ![]() und
und ![]() . Durch die Substitution
. Durch die Substitution
erhält man eine Zufallsgröße ![]() , die der normierten Normalverteilung genügt. Für diese gilt
, die der normierten Normalverteilung genügt. Für diese gilt
Gibt man jetzt eine Irrtumswahrscheinlichkeit ![]() vor und verlangt
vor und verlangt
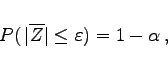 |
(16.139) |
dann kann man ![]() aus (16.138) numerisch bestimmen bzw. aus der Tabelle Normierte Normalverteilung ablesen und erhält aus
aus (16.138) numerisch bestimmen bzw. aus der Tabelle Normierte Normalverteilung ablesen und erhält aus ![]() unter Beachtung von (16.137) die Beziehung
unter Beachtung von (16.137) die Beziehung
Die Werte  in (16.140) heißen Vertrauensgrenzen für den Mittelwert
in (16.140) heißen Vertrauensgrenzen für den Mittelwert ![]() der Grundgesamtheit bei bekannter Streuung
der Grundgesamtheit bei bekannter Streuung ![]() und vorgegebener Irrtumswahrscheinlichkeit
und vorgegebener Irrtumswahrscheinlichkeit ![]() . Man kann auch sagen: Der Mittelwert
. Man kann auch sagen: Der Mittelwert ![]() liegt mit der statistischen Sicherheit
liegt mit der statistischen Sicherheit ![]() zwischen den Vertrauensgrenzen (16.140).
zwischen den Vertrauensgrenzen (16.140).
Hinweis: Ist der Stichprobenumfang hinreichend groß ![]() , dann kann in (16.140) an Stelle der in der Regel unbekannten Streuung
, dann kann in (16.140) an Stelle der in der Regel unbekannten Streuung ![]() der Grundgesamtheit die Stichprobenstreuung s2 verwendet werden. Anderenfalls müssen die Vertrauensgrenzen mit Hilfe der t-Verteilung gemäß (16.143) ermittelt werden.
der Grundgesamtheit die Stichprobenstreuung s2 verwendet werden. Anderenfalls müssen die Vertrauensgrenzen mit Hilfe der t-Verteilung gemäß (16.143) ermittelt werden.