Inhalt Index DeskTop Bronstein
![]()
![]() Wahrscheinlichkeitsrechnung und Mathematische Statistik Mathematische Statistik Wichtige Prüfverfahren
Wahrscheinlichkeitsrechnung und Mathematische Statistik Mathematische Statistik Wichtige Prüfverfahren
Die Zufallsgröße X sei normalverteilt mit den Parametern ![]() und
und ![]() . Dann genügt die neue Zufallsgröße
. Dann genügt die neue Zufallsgröße
einer ![]() -Verteilung mit m=n - 1 Freiheitsgraden, wobei n der Umfang einer Stichprobe ist und s2 deren Streuung. Aus der folgenden Abbildung, in der
-Verteilung mit m=n - 1 Freiheitsgraden, wobei n der Umfang einer Stichprobe ist und s2 deren Streuung. Aus der folgenden Abbildung, in der ![]() die Wahrscheinlichkeitsdichte der
die Wahrscheinlichkeitsdichte der ![]() -Verteilung bedeutet, folgt
-Verteilung bedeutet, folgt
 |
(16.145) |
d.h., mit den Quantilen der ![]() -Verteilung besteht der Zusammenhang (s. Tabelle Chi-Quadrat-Verteilung):
-Verteilung besteht der Zusammenhang (s. Tabelle Chi-Quadrat-Verteilung):
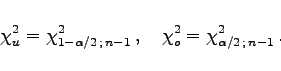 |
(16.146) |
Unter Beachtung von (16.144) erhält man damit die folgende Abschätzung für die unbekannte Streuung ![]() der Grundgesamtheit bei einer Irrtumswahrscheinlichkeit
der Grundgesamtheit bei einer Irrtumswahrscheinlichkeit ![]() :
:
Das durch (16.147) beschriebene Vertrauensintervall für ![]() wird bei kleinem Stichprobenumfang noch sehr grob sein.
wird bei kleinem Stichprobenumfang noch sehr grob sein.
| Beispiel |
|
Für die Zahlenwerte des Beispiels Stichprobe mit 6 Meßwerten und |