Inhalt Index DeskTop Bronstein
![]()
![]() Wahrscheinlichkeitsrechnung und Mathematische Statistik Mathematische Statistik Wichtige Prüfverfahren
Wahrscheinlichkeitsrechnung und Mathematische Statistik Mathematische Statistik Wichtige Prüfverfahren
Ein statistisches Prüfverfahren hat grundsätzlich folgenden Aufbau:
| Beispiel |
|
Prüfen des Mittelwertes mit der Hypothese H: |
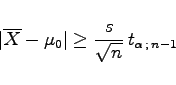 |
(16.148) |
ergibt. Man sagt dann, es handelt sich um eine signifikante Abweichung und spricht von Signifikanz.
Weitere Angaben über die Durchführung von Prüfverfahren s. [16.24].