Klassifizierung periodischer Orbits

Hat der periodische Orbit von (17.1) außer keinen weiteren Multiplikator auf dem komplexen Einheitskreis, so heißt hyperbolisch. Der hyperbolische periodische Orbit heißt vom Typ , wenn m Multiplikatoren innerhalb und k =n-1 Multiplikatoren außerhalb des Einheitskreises liegen. Ist m > 0 und , so heißt der periodische Orbit vom Typ (m, k) sattelartig.

Nach einem Satz von ANDRONOV und WITT ist ein hyperbolischer periodischer Orbit von (17.1) vom Typ (n-1, 0) asymptotisch stabil. Hyperbolische periodische Orbits vom Typ (m, k) mit k >0 sind instabil.

Beispiel A

Ein periodischer Orbit in der Ebene mit den Multiplikatoren und ist asymptotisch stabil, wenn , d.h. wenn ist.

Liegt außer noch ein weiterer Multiplikator auf dem komplexen Einheitskreis, so ist der Satz von ANDRONOV-WITT nicht anwendbar. Zur Stabilitätsanalyse des periodischen Orbits reichen die Informationen über die Multiplikatoren nicht aus.

Beispiel B

Als Beispiel sei das ebene System 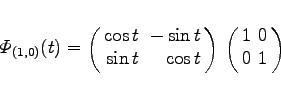mit der glatten Funktion gegeben, die zusätzlich den Eigenschaften f(1) = f'(1)=0 und f(r)(r-1) < 0 für alle , genügt. Offenbar ist eine -periodische Lösung des betrachteten Systems und

die FLOQUET-Darstellung der Fundamentalmatrix. Aus ihr erkennt man, daß ist. Die Verwendung von Polarkoordinaten führt zum System . Aus dieser Darstellung folgt sofort, daß der periodische Orbit asymptotisch stabil ist.