Stabilität periodischer Orbits

Sei eine T-periodische Lösung von (17.1) und ihr Orbit. Das Phasenporträt nahe wird, unter gewissen Voraussetzungen, durch die Variationsgleichung beschrieben. Da eine T-periodische stetige Matrixfunktion vom Typ (n,n) ist, folgt aus dem Satz von FLOQUET, daß die bei t = 0 normierte Fundamentalmatrix der Variationsgleichung als darstellbar ist, wobei G eine T-periodische reguläre glatte Matrixfunktion mit G(0) = E_n ist und R eine konstante Matrix vom Typ (n,n) darstellt, die nicht eindeutig festliegt. Die Matrix heißt Monodromie-Matrix des periodischen Orbits , die Eigenwerte von e^RT sind die Multiplikatoren des periodischen Orbits . Wird der Orbit durch eine andere Lösung repräsentiert, d.h., ist , so stimmen die Multiplikatoren von und überein. Einer der Multiplikatoren eines periodischen Orbits ist immer gleich Eins (Satz von ANDRONOV-WITT).

Seien die Multiplikatoren des periodischen Orbits , und sei die Monodromie-Matrix von . Dann gilt

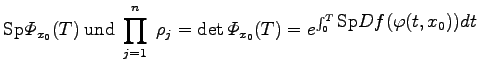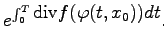= (17.17)

Ist also , so ist und .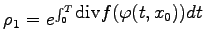

Beispiel

Sei 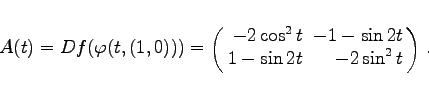eine -periodische Lösung von (17.9a). Die Matrix A(t) der Variationsgleichung lautet

Die bei t = 0 normierte Fundamentalmatrix ist

wobei das letzte Produkt eine FLOQUET-Darstellung von darstellt. Also ist und . Die Multiplikatoren lassen sich auch ohne FLOQUET-Darstellung bestimmen. Für System (17.9a) ist div. Damit ergibt sich div. Nach obiger Formel ist .