Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Wahrscheinlichkeitsmaße auf Attraktoren Elemente der Ergodentheorie
Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Wahrscheinlichkeitsmaße auf Attraktoren Elemente der Ergodentheorie
Das dynamische System ![]() auf M mit invariantem Maß
auf M mit invariantem Maß ![]() sei ergodisch. Es seien
sei ergodisch. Es seien ![]() eine beliebige stetige Funktion,
eine beliebige stetige Funktion, ![]() ein beliebiger Semiorbit und das räumliche Mittel
ein beliebiger Semiorbit und das räumliche Mittel ![]() sei ersetzt durch das zeitliche Mittel, d.h. durch
sei ersetzt durch das zeitliche Mittel, d.h. durch 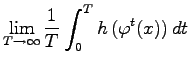 im zeitkontinuierlichen Fall und durch
im zeitkontinuierlichen Fall und durch ![]() im zeitdiskreten Fall. Bezüglich h wird die Autokorrelationsfunktion längs des Semiorbits
im zeitdiskreten Fall. Bezüglich h wird die Autokorrelationsfunktion längs des Semiorbits ![]() zu einem Zeitpunkt
zu einem Zeitpunkt ![]() für einen Fluß durch
für einen Fluß durch
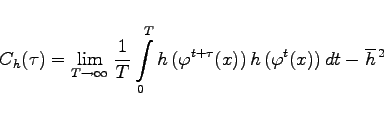 |
(17.34a) |
und für ein zeitdiskretes System durch
 |
(17.34b) |
definiert. Die Autokorrelationsfunktion wird auch für negative Zeiten erklärt, indem ![]() als gerade Funktion auf
als gerade Funktion auf ![]() bzw.
bzw. ![]() aufgefaßt wird.
aufgefaßt wird.
Periodische oder quasiperiodische Orbits führen zu einem periodischen bzw. quasiperiodischen Verhalten von ![]() . Ein schneller Abfall von
. Ein schneller Abfall von ![]() für wachsende
für wachsende ![]() und beliebiger Testfunktion h deutet auf chaotisches Verhalten hin. Fällt
und beliebiger Testfunktion h deutet auf chaotisches Verhalten hin. Fällt ![]() für wachsende
für wachsende ![]() sogar mit exponentieller Geschwindigkeit, so ist dies ein Anzeichen für mischendes Verhalten.
sogar mit exponentieller Geschwindigkeit, so ist dies ein Anzeichen für mischendes Verhalten.