Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Wahrscheinlichkeitsmaße auf Attraktoren Elemente der Ergodentheorie
Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Wahrscheinlichkeitsmaße auf Attraktoren Elemente der Ergodentheorie
Ein dynamisches System ![]() auf
auf ![]() mit invariantem Wahrscheinlichkeitsmaß
mit invariantem Wahrscheinlichkeitsmaß ![]() heißt mischend, wenn
heißt mischend, wenn ![]() für beliebige BOREL-Mengen
für beliebige BOREL-Mengen ![]() gilt. Für ein mischendes System hängt also das Maß der Menge aller Punkte, die bei t=0 in A und für große t in B liegen, nur vom Produkt
gilt. Für ein mischendes System hängt also das Maß der Menge aller Punkte, die bei t=0 in A und für große t in B liegen, nur vom Produkt ![]() ab.
ab.
Ein mischendes System ist auch ergodisch: Seien ![]() ein mischendes System und A eine BOREL-Menge mit
ein mischendes System und A eine BOREL-Menge mit ![]() . Dann gilt
. Dann gilt ![]() und
und ![]() ist 0 oder
ist 0 oder ![]() .
.
Ein Fluß ![]() von (17.1) ist genau dann mischend, wenn für beliebige quadratisch integrierbare Funktionen
von (17.1) ist genau dann mischend, wenn für beliebige quadratisch integrierbare Funktionen ![]() die Beziehung
die Beziehung
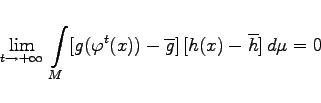 |
(17.33) |
gilt. Dabei bezeichnen ![]() und
und ![]() die räumlichen Mittel, die durch die zeitlichen Mittel ersetzt werden.
die räumlichen Mittel, die durch die zeitlichen Mittel ersetzt werden.
| Beispiel |
|
Die Modulo-Abbildung (17.28) ist mischend. Die Rotationsabbildung (17.31) ist bezüglich des Wahrscheinlichkeitsmaßes |