Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Wahrscheinlichkeitsmaße auf Attraktoren Elemente der Ergodentheorie
Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Wahrscheinlichkeitsmaße auf Attraktoren Elemente der Ergodentheorie
Die FOURIER-Transformierte von ![]() heißt Leistungsspektrum (s. auch Spektralinterpretation) und wird mit
heißt Leistungsspektrum (s. auch Spektralinterpretation) und wird mit ![]() bezeichnet. Im zeitkontinuierlichen Fall gilt unter der Voraussetzung
bezeichnet. Im zeitkontinuierlichen Fall gilt unter der Voraussetzung
 :
:
 |
(17.35a) |
Im zeitdiskreten Fall ist, falls  gilt:
gilt:
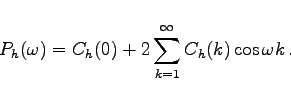 |
(17.35b) |
Liegt die absolute Integrierbarkeit bzw. Summierbarkeit von ![]() nicht vor, kann in wichtigen Fällen Ph als Distribution aufgefaßt werden. Periodischen Bewegungen eines dynamischen Systems entspricht ein Leistungsspektrum, das durch äquidistante Impulse charakterisiert ist. Bei quasiperiodischen Bewegungen treten im Leistungsspektrum Impulse auf, die sich aus ganzzahligen Linearkombinationen der Grundimpulse der quasiperiodischen Bewegung ergeben. Ein breitbandiges Spektrum mit einzelnen Spitzen kann dagegen als Indikator für chaotisches Verhalten gelten.
nicht vor, kann in wichtigen Fällen Ph als Distribution aufgefaßt werden. Periodischen Bewegungen eines dynamischen Systems entspricht ein Leistungsspektrum, das durch äquidistante Impulse charakterisiert ist. Bei quasiperiodischen Bewegungen treten im Leistungsspektrum Impulse auf, die sich aus ganzzahligen Linearkombinationen der Grundimpulse der quasiperiodischen Bewegung ergeben. Ein breitbandiges Spektrum mit einzelnen Spitzen kann dagegen als Indikator für chaotisches Verhalten gelten.
| Beispiel A |
|
Seien |
| Beispiel B |
|
Seien |