Fraktale

Attraktoren oder andere invariante Mengen von dynamischen Systemen können geometrisch komplizierter als Punkt, Linie oder Torus aufgebaut sein. Fraktale sind, auch unabhängig von einer Dynamik, Mengen, die sich durch eines oder mehrere Merkmale wie Ausfransung, Porösität, Komplexität, Selbstähnlichkeit auszeichnen. Da der übliche Dimensionsbegriff, wie er für glatte Flächen und Kurven gebraucht wird, für Fraktale nicht anwendbar ist, müssen verallgemeinerte Definitionen der Dimension herangezogen werden. Eine ausführlichere Darstellung der Dimensionstheorie s. [17.8], [17.20].

Beispiel

Das Intervall G₀ =[0,1] wird in drei Teilintervalle gleicher Länge geteilt und das mittlere offene Drittel entfernt, so daß die Menge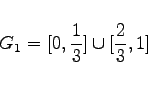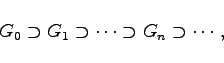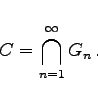

entsteht. Dann werden von den beiden Teilintervallen von G₁ die jeweils mittleren offenen Drittel entfernt, so daß die Menge

entsteht. Diese Prozedur wird mit G_k fortgesetzt, indem aus jedem Teilintervall von G_k-1 das mittlere offene Drittel entfernt wird. Dadurch entsteht eine Folge von Mengen

wobei jedes G_n aus 2ⁿ Intervallen der Länge besteht. Die CANTOR-Menge C ist definiert als Menge aller der Punkte, die allen G_n angehören, d.h.,

Die Menge C ist kompakt, überabzählbar, hat das LEBESGUE-Maß Null und ist perfekt. D.h., C ist abgeschlossen, und jeder Punkt ist Häufungspunkt. Die CANTOR-Menge kann als Beispiel für ein Fraktal dienen.