Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Dimensionen Metrische Dimensionen
Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Dimensionen Metrische Dimensionen
Die Motivation für diese Dimension ergibt sich aus der Volumenberechnung durch das LEBESGUE-Maß. Wird eine beschränkte Menge ![]() mit einer Überdeckung aus einer endlichen Anzahl Kugeln Bri mit Radius
mit einer Überdeckung aus einer endlichen Anzahl Kugeln Bri mit Radius ![]() versehen, so daß also
versehen, so daß also ![]() gilt, erhält man für A das Rohvolumen
gilt, erhält man für A das Rohvolumen ![]() . Bildet man nun über alle endlichen Überdeckungen von A durch Kugeln mit Radius
. Bildet man nun über alle endlichen Überdeckungen von A durch Kugeln mit Radius ![]() die Größe
die Größe ![]() und läßt
und läßt ![]() gegen Null gehen, so ergibt sich das äußere LEBESGUE-Maß
gegen Null gehen, so ergibt sich das äußere LEBESGUE-Maß ![]() von
von ![]() , das für meßbare Mengen mit dem Volumen vol(A) übereinstimmt.
, das für meßbare Mengen mit dem Volumen vol(A) übereinstimmt.
Es seien M der EUKLIDische Raum ![]() oder, allgemeiner, ein separabler metrischer Raum mit Metrik
oder, allgemeiner, ein separabler metrischer Raum mit Metrik ![]() und
und ![]() eine Teilmenge. Für beliebige Parameter
eine Teilmenge. Für beliebige Parameter ![]() und
und ![]() wird die Größe
wird die Größe
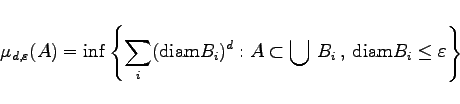 |
(17.40a) |
gebildet, wobei ![]() beliebige Teilmengen mit Durchmesser diam
beliebige Teilmengen mit Durchmesser diam![]() sind. Das äußere HAUSDORFF-Maß zur Dimension d von A wird durch
sind. Das äußere HAUSDORFF-Maß zur Dimension d von A wird durch
 |
(17.40b) |
definiert und kann endlich oder unendlich sein. Die HAUSDORFF-Dimension dH(A) der Menge A ist dann der (einzige) kritische Wert des HAUSDORFF-Maßes:
 |
(17.40c) |
Bemerkung: Die Größen ![]() können auch mit Hilfe von Überdeckungen aus Kugeln vom Radius
können auch mit Hilfe von Überdeckungen aus Kugeln vom Radius ![]() oder, im Falle des
oder, im Falle des ![]() , aus Würfeln der Kantenlänge
, aus Würfeln der Kantenlänge ![]() gebildet werden.
gebildet werden.
Wichtige Eigenschaften der Hausdorff-Dimension:
| Beispiel |
|
Für die Menge |