Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Dimensionen Metrische Dimensionen
Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Dimensionen Metrische Dimensionen
Sei A im weiteren eine relativ kompakte Menge des metrischen Raumes ![]() und sei
und sei ![]() die minimale Anzahl von Mengen vom Durchmesser
die minimale Anzahl von Mengen vom Durchmesser ![]() , die nötig ist, um A zu überdecken. Die Größe
, die nötig ist, um A zu überdecken. Die Größe
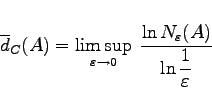 |
(17.41a) |
heißt obere Kapazitätsdimension oder fraktale Dimension, die Größe
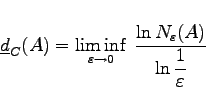 |
(17.41b) |
heißt untere Kapazitätsdimension von ![]() . Gilt
. Gilt ![]() , so heißt dC(A) Kapazitätsdimension von
, so heißt dC(A) Kapazitätsdimension von ![]() .
.
Für eine beschränkte Menge ![]() kann in den obigen Definitionen die Zahl
kann in den obigen Definitionen die Zahl ![]() auch folgendermaßen definiert werden: Der
auch folgendermaßen definiert werden: Der ![]() wird mit einem Gitter aus n-dimensionalen Würfeln der Seitenlänge
wird mit einem Gitter aus n-dimensionalen Würfeln der Seitenlänge ![]() überdeckt. Dann kann für
überdeckt. Dann kann für ![]() die Anzahl der Würfel des Gitters, die A schneiden, genommen werden.
die Anzahl der Würfel des Gitters, die A schneiden, genommen werden.
Wichtige Eigenschaften der Kapazitätsdimension:
| Beispiel |
|
Sei |