Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Dimensionen
Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Dimensionen
Sei ![]() ein glattes dynamisches System auf
ein glattes dynamisches System auf ![]() und
und ![]() eine kompakte invariante Menge. Ein beliebiges
eine kompakte invariante Menge. Ein beliebiges ![]() werde fixiert und
werde fixiert und ![]() gesetzt.
gesetzt.
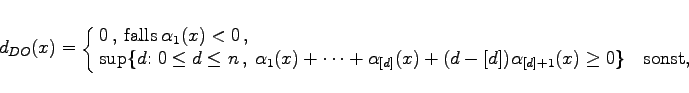 |
(17.50) |
wobei ![]() beliebig ist und [d] den ganzzahligen Anteil von d bedeutet, heißt DOUADY-OESTERL´E-Dimension im Punkt
beliebig ist und [d] den ganzzahligen Anteil von d bedeutet, heißt DOUADY-OESTERL´E-Dimension im Punkt ![]() . Unter den Voraussetzungen des oben formulierten Satzes von DOUADY-OESTERL´E für Differentialgleichungen gilt dann
. Unter den Voraussetzungen des oben formulierten Satzes von DOUADY-OESTERL´E für Differentialgleichungen gilt dann ![]() .
.
| Beispiel |
|
Das LORENZ-System (17.2) besitzt für
(Die Abbildung wurde mit Mathematica erzeugt.) |