Dissipative Bäcker-Abbildung

Sei ein Parameter und M =[0,1] x [0,1] das Einheitsquadrat. Die Abbildung

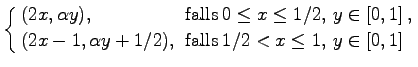= (17.51)

heißt dissipative Bäcker-Abbildung. Zwei Iterationen der Bäcker-Abbildung sind in der folgenden Abbildung zu sehen.

Man erkennt die entstehende Blätterteigstruktur . Die Menge 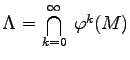ist invariant unter und alle Punkte aus M werden von angezogen. Der Wert für die HAUSDORFF-Dimension ist . Für das dynamische System existiert auf M ein invariantes Maß , verschieden vom LEBESGUE-Maß. In den Punkten, wo die Ableitungen existieren, erhält man die JACOBI-Matrizen 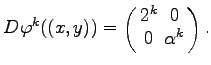Hieraus ergeben sich die Singulärwerte und, demzufolge, die LYAPUNOV-Exponenten (bezüglich des invarianten Maßes . Damit gilt für die LYAPUNOV-Dimension
. Die PESINsche Formel für die metrische Entropie stimmt hier, d.h., es gilt 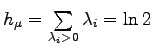.