Inhalt Index DeskTop Bronstein
![]()
![]() Numerische Mathematik Numerische Lösung von Gleichungssystemen Lineare Gleichungssysteme Dreieckszerlegung einer Matrix
Numerische Mathematik Numerische Lösung von Gleichungssystemen Lineare Gleichungssysteme Dreieckszerlegung einer Matrix
Das Ergebnis des GAUSSschen Eliminationsverfahrens kann wie folgt formuliert werden: Zu jeder regulären Matrix ![]() existiert eine sogenannte Dreieckszerlegung oder LR-Faktorisierung der Form
existiert eine sogenannte Dreieckszerlegung oder LR-Faktorisierung der Form
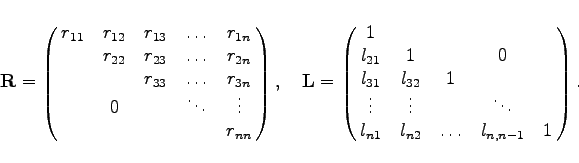 |
(19.32) |
![]() heißt Rechtsdreiecksmatrix,
heißt Rechtsdreiecksmatrix, ![]() Linksdreiecksmatrix und
Linksdreiecksmatrix und ![]() ist eine sogenannte Permutationsmatrix. Sie ist eine quadratische Matrix, die in jeder Zeile und in jeder Spalte genau eine 1 und sonst Nullen enthält. Sie beschreibt die Zeilenvertauschungen in der Matrix
ist eine sogenannte Permutationsmatrix. Sie ist eine quadratische Matrix, die in jeder Zeile und in jeder Spalte genau eine 1 und sonst Nullen enthält. Sie beschreibt die Zeilenvertauschungen in der Matrix ![]() , die sich durch die Pivotwahl in den Eliminationsschritten ergeben.
, die sich durch die Pivotwahl in den Eliminationsschritten ergeben.
| Beispiel |
|
Das GAUSSsche Eliminationsverfahren soll auf das System |