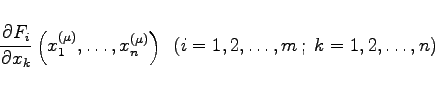Inhalt Index DeskTop Bronstein
![]()
![]() Numerische Mathematik Numerische Lösung von Gleichungssystemen Nichtlineare Gleichungssysteme
Numerische Mathematik Numerische Lösung von Gleichungssystemen Nichtlineare Gleichungssysteme
Zur Lösung der Quadratmittelaufgabe (19.24) geht man im nichtlinearen Fall (nichtlineare Ausgleichsaufgabe) iterativ wie folgt vor:
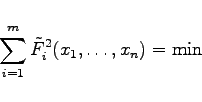 |
(19.66) |
z.B. mit Hilfe der Normalgleichungen (19.42), oder des HOUSEHOLDER-Verfahrens.
Wenn die Berechnung der partiellen Ableitungen