Inhalt Index DeskTop Bronstein
![]()
![]() Numerische Mathematik Numerische Lösung nichtlinearer Gleichungen Iterationsverfahren
Numerische Mathematik Numerische Lösung nichtlinearer Gleichungen Iterationsverfahren
d.h., es benötigt zur Berechnung des neuen Näherungswertes xn+1 die Werte der Funktion f(x) und ihrer 1. Ableitung f'(x) an der Stelle ![]() .
.
erforderlich, die Bedingung
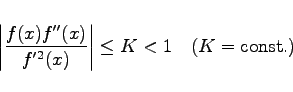 |
(19.7b) |
hinreichend. Die Bedingungen (19.7a,b) müssen in einer Umgebung von ![]() , die alle Punkte xn enthält, erfüllt sein. Falls das NEWTON-Verfahren konvergiert, dann konvergiert es so gut, daß sich bei jedem Iterationsschritt die Anzahl der genauen Stellen etwa verdoppelt. Man spricht in diesem Fall auch von quadratischer Konvergenz.
, die alle Punkte xn enthält, erfüllt sein. Falls das NEWTON-Verfahren konvergiert, dann konvergiert es so gut, daß sich bei jedem Iterationsschritt die Anzahl der genauen Stellen etwa verdoppelt. Man spricht in diesem Fall auch von quadratischer Konvergenz.
| Beispiel |
|
Zur Lösung der Gleichung |
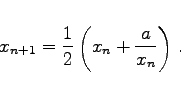 |
(19.8) |
Für a=2 erhält man:
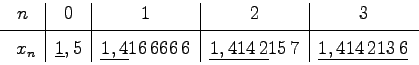
Die Grundidee des NEWTON-Verfahrens besteht in der lokalen Approximation der Kurve y = f(x) durch eine Tangente.
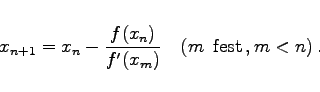 |
(19.9) |
Die Güte der Konvergenz wird durch diese Vereinfachung nicht wesentlich beeinflußt.