Inhalt Index DeskTop Bronstein
![]()
![]() Numerische Mathematik Genäherte Integration von partiellen Differentialgleichungen
Numerische Mathematik Genäherte Integration von partiellen Differentialgleichungen
Das Integrationsgebiet wird durch ausgewählte Punkte ![]() gitterförmig unterteilt. Gewöhnlich wird das Gitter rechteckig gewählt:
gitterförmig unterteilt. Gewöhnlich wird das Gitter rechteckig gewählt:
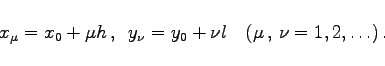 |
(19.136) |
Für l=h erhält man ein quadratisches Gitter. Bezeichnet man die gesuchte Lösung mit ![]() , dann werden die in der Differentialgleichung und in den Rand- bzw. Anfangsbedingungen auftretenden partiellen Ableitungen durch finite Ausdrücke der folgenden Art ersetzt, wobei unter
, dann werden die in der Differentialgleichung und in den Rand- bzw. Anfangsbedingungen auftretenden partiellen Ableitungen durch finite Ausdrücke der folgenden Art ersetzt, wobei unter ![]() ein Näherungswert für den Funktionswert
ein Näherungswert für den Funktionswert ![]() zu verstehen ist:
zu verstehen ist:
In (19.137) ist die Fehlerordnung mit Hilfe des LANDAU-Symbols O angegeben worden.
Insbesondere bei parabolischen Differentialgleichungen ist es günstiger, die Näherung
mit einem festen Parameter ![]()
![]() zu verwenden. Die Formel (19.138) stellt eine Konvexkombination zweier finiter Ausdrücke dar, die aus der entsprechenden Formel von (19.137) für die Werte
zu verwenden. Die Formel (19.138) stellt eine Konvexkombination zweier finiter Ausdrücke dar, die aus der entsprechenden Formel von (19.137) für die Werte ![]() und
und ![]() enstanden sind.
enstanden sind.
Mit den Formeln (19.137) kann eine partielle Differentialgleichung für jeden inneren Gitterpunkt in eine Differenzengleichung übergeführt werden, wobei die Rand- und Anfangsbedingungen zu beachten sind. Das so entstehende Gleichungssystem für die Näherungswerte ![]() , das für kleine Schrittweiten h und l von großer Dimension ist, muß in der Regel iterativ gelöst werden
, das für kleine Schrittweiten h und l von großer Dimension ist, muß in der Regel iterativ gelöst werden
(s. Abschnitt Iteration in Gesamt- und Einzelschritten).
| Beispiel B |
|
Die Gleichungssysteme, die bei der Anwendung des Differenzenverfahrens auf partielle Differentialgleichungen entstehen, haben in der Regel eine sehr spezielle Struktur. Das soll am Beispiel der folgenden, etwas allgemeineren Randwertaufgabe gezeigt werden. Integrationsgebiet sei das Quadrat 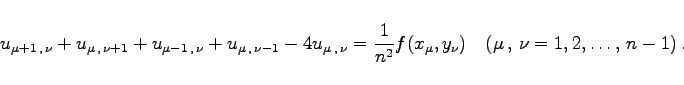 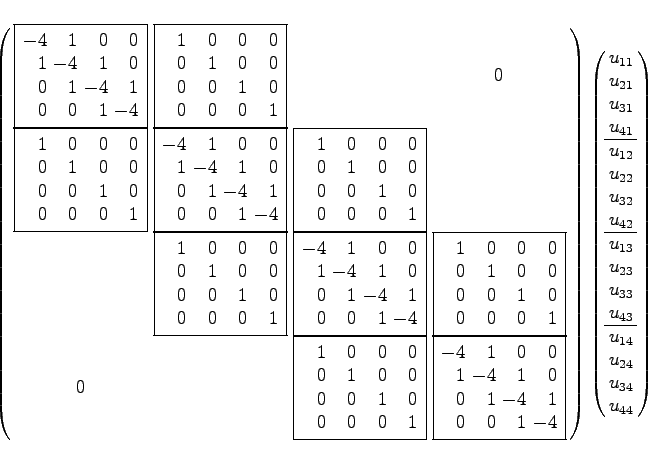 Man sieht: Die Koeffizientenmatrix ist symmetrisch und schwach besetzt. Ihre Gestalt wird als block-tridiagonal bezeichnet. Man beachte aber, daß die Gestalt der Koeffizientenmatrix davon abhängig ist, wie die Gitterpunkte durchlaufen werden. |
Für die verschiedenen Aufgabenklassen bei partiellen Differentialgleichungen 2. Ordnung, insbesondere bei elliptischen, parabolischen und hyperbolischen Differentialgleichungen, ist eine Vielzahl angepaßter Differenzenverfahren entwickelt und auf Konvergenz und Stabilität hin untersucht worden. Die Spezialliteratur dazu ist umfangreich, Standardwerke s. [19.28], [19.31], [19.20].