Reelle Argumentwerte

Zur Berechnung des Funktionswertes pn(x0) eines Polynoms n-ten Grades an der Stelle x = x0 aus seinen Koeffizienten geht man von der Beziehung

(19.12)

aus, wobei pn-1(x) ein Polynom vom Grade n-1 ist:

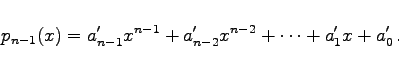(19.13)

Durch Koeffizientenvergleich in (19.12) bezüglich xk erhält man die Rekursionsformel

(19.14)

Auf diese Weise werden aus den Koeffizienten ak von pn(x) die Koeffizienten ak' von pn-1(x) sowie der gesuchte Funktionswert pn(x0) bestimmt. Durch Wiederholung dieser Vorgehensweise, d.h., im nächsten Schritt wird das Polynom pn-1(x) mit dem Polynom pn-2(x) gemäß

pn-1(x) = (x-x0)pn-2(x)+pn-1(x0) (19.15)


verknüpft usw., erhält man schließlich eine Folge von Polynomen . Die Berechnung der Koeffizienten und Funktionswerte dieser Polynome ist in (19.16) schematisch dargestellt:
(19.16)

Aus dem Schema (19.16) liest man pn(x0) unmittelbar ab. Darüber hinaus gilt:

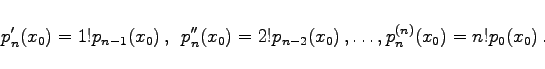(19.17)
Beispiel

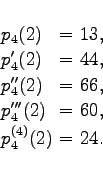. Der Funktionswert und die Ableitungswerte von p4(x) an der Stelle x0 = 2 sind gemäß (19.16) zu berechnen.


Man liest ab

Hinweis: Das HORNER-Schema läßt sich auch für komplexe Koeffizienten ak durchführen, indem man für jeden Koeffizienten eine reelle und eine imaginäre Spalte gemäß (19.16) berechnet.