Inhalt Index DeskTop Bronstein
![]()
![]() Numerische Mathematik Numerische Lösung nichtlinearer Gleichungen Lösung von Polynomgleichungen Horner-Schema
Numerische Mathematik Numerische Lösung nichtlinearer Gleichungen Lösung von Polynomgleichungen Horner-Schema
Sind die Koeffizienten ak in (19.11) reell, so kann die Berechnung von pn(x0) für komplexe Werte ![]() ganz im Reellen ablaufen. Dazu wird pn(x) wie folgt zerlegt:
ganz im Reellen ablaufen. Dazu wird pn(x) wie folgt zerlegt:
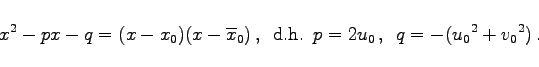 |
(19.18b) |
Es ist dann
 |
(19.18c) |
Zur Realisierung von (19.18a) kann man nach COLLATZ das folgende sogenannte zweizeilige HORNER-Schema aufstellen:
 |
(19.18d) |
| Beispiel |
|
p4(x)=x4+2x3-3x2-7. Der Funktionswert für |