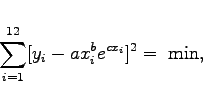Inhalt Index DeskTop Bronstein
![]()
![]() Funktionen und ihre Darstellung Aufstellung empirischer Kurven Gebräuchlichste empirische Formeln
Funktionen und ihre Darstellung Aufstellung empirischer Kurven Gebräuchlichste empirische Formeln
| x | y | yerr | |||||||
| 0,1 | 1,78 | 0,056 | 0,007 | -1,000 | 0,250 | 0,301 | 0,252 | 0,252 | 1,78 |
| 0,2 | 3,18 | 0,063 | 0,031 | -0,699 | 0,502 | 0,176 | +0,002 | -0,097 | 3,15 |
| 0,3 | 3,19 | 0,094 | 0,063 | -0,523 | 0,504 | 0,125 | -0,099 | -0,447 | 3,16 |
| 0,4 | 2,54 | 0,157 | 0,125 | -0,398 | 0,405 | 0,097 | -0,157 | -0,803 | 2,52 |
| 0,5 | 1,77 | 0,282 | 0,244 | -0,301 | 0,248 | 0,079 | -0,191 | -1,134 | 1,76 |
| 0,6 | 1,14 | 0,526 | 0,488 | -0,222 | 0,057 | 0,067 | -0,218 | -1,455 | 1,14 |
| 0,7 | 0,69 | 1,014 | 0,986 | -0,155 | -0,161 | 0,058 | -0,237 | - | 0,70 |
| 0,8 | 0,40 | 2,000 | 1,913 | -0,097 | -0,398 | 0,051 | -0,240 | - | 0,41 |
| 0,9 | 0,23 | 3,913 | 3,78 | -0,046 | -0,638 | 0,046 | -0,248 | - | 0,23 |
| 1,0 | 0,13 | 7,69 | 8,02 | 0,000 | -0,886 | 0,041 | -0,269 | - | 0,13 |
| 1,1 | 0,07 | 15,71 | 14,29 | 0,041 | -1,155 | 0,038 | -0,243 | - | 0,07 |
| 1,2 | 0,04 | 30,0 | - | 0,079 | -1,398 | - | - | - | 0,04 |
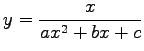 (2.253) oder y=axbecx (2.255a) mit den folgenden Abbildungen geeignet sein könnten.
(2.253) oder y=axbecx (2.255a) mit den folgenden Abbildungen geeignet sein könnten.
In beiden Fällen ist die Übereinstimmung mit einer Geraden ausreichend, so daß die Formel y=axbecx für die Näherung geeignet ist. Zur Bestimmung der Konstanten a,b und c wird eine lineare Abhängigkeit zwischen x und ![]() mit der Mittelwertmethode gesucht. Addition der Bedingungsgleichungen
mit der Mittelwertmethode gesucht. Addition der Bedingungsgleichungen ![]() in zwei Gruppen zu je drei Gleichungen führt auf
in zwei Gruppen zu je drei Gleichungen führt auf