Inhalt Index DeskTop Bronstein
![]()
![]() Geometrie Sphärische Trigonometrie Berechnung sphärischer Dreiecke Schiefwinklig sphärisches Dreieck
Geometrie Sphärische Trigonometrie Berechnung sphärischer Dreiecke Schiefwinklig sphärisches Dreieck
Gegeben: 2 Winkel und die einem Winkel gegenüberliegende Seite, z.B. ![]()
Bedingungen: Siehe Fallunterscheidung.
Lösung: Gesucht beliebige fehlende Größe .
 |
(3.227) |
2 Werte b1, b2 sind möglich. Es sei b1 spitz und ![]() stumpf.
stumpf.
Fallunterscheidung:
 d.h. 0 Lösungen.
d.h. 0 Lösungen.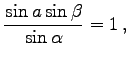 d.h. 1 Lösung
d.h. 1 Lösung  d.h. weitere Fallunterscheidungen sind notwendig:
d.h. weitere Fallunterscheidungen sind notwendig:Fortführung: Weitere Berechnung mit einer Seite oder 2 Seiten ![]() .
.
Dazu wird von C das sphärische Lot auf AB bis D gefällt.
 |
(3.228a) |
 |
(3.228b) |
 |
(3.228c) |
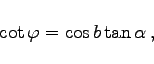 |
(3.228d) |
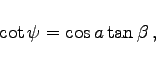 |
(3.228e) |
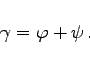 |
(3.228f) |
 |
(3.229a) |
 |
(3.229b) |

| Beispiel A: Dreiseitige Pyramide |
|
Eine dreiseitige Pyramide hat die Grundfläche ABC und die Spitze
Die Seitenflächen ABS und BCS schneiden sich unter
|
| Beispiel B: Funkpeilung |
|
Durch Funkpeilung von zwei festen Stationen Gesucht sind die geographischen Koordinaten des Standortes P0 des Schiffes. Die in der Nautik unter dem Namen Fremdpeilung bekannte Aufgabe stellt einen Vorwärtseinschnitt auf der Kugel dar und wird ähnlich dem Vorwärtseinschnitt in der Ebene gelöst.
|