Linearkombinationen von Vektoren
- a) Die Summe zweier Vektoren
 und
und  ist ein Vektor
ist ein Vektor  der die Diagonale
der die Diagonale  des Parallelogramms ABCD bildet. Die wichtigsten Eigenschaften der Summe zweier Vektoren sind das Kommutativgesetz der Addition und die Dreiecksungleichung:
des Parallelogramms ABCD bildet. Die wichtigsten Eigenschaften der Summe zweier Vektoren sind das Kommutativgesetz der Addition und die Dreiecksungleichung:
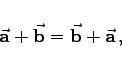 |
(3.262a) |
 |
(3.262b) |
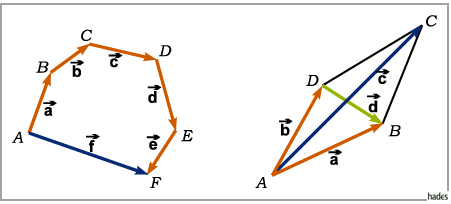
- b) Die Summe mehrerer Vektoren
 ist ein Vektor
ist ein Vektor  der den Polygonzug schließt, den die Vektoren
der den Polygonzug schließt, den die Vektoren  bis
bis  bilden. Für n Vektoren
bilden. Für n Vektoren  gilt:
gilt:
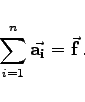 |
(3.262c) |
Zu den Eigenschaften der Summe mehrer Vektoren gehören das Kommutativgesetz der Addition und das Assoziativgesetz der Addition. Für drei Vektoren z.B gilt:
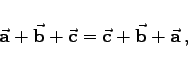 |
(3.262d) |
 |
(3.262e) |
- c) Die Differenz zweier Vektoren
 kann als Summe der Vektoren
kann als Summe der Vektoren  und
und  aufgefaßt werden, so daß
aufgefaßt werden, so daß
 |
(3.262f) |
die Diagonale  in der linken Abbildung ergibt.
in der linken Abbildung ergibt.

Die wichtigsten Eigenschaften der Differenz zweier Vektoren sind:
 |
(3.262g) |
![]()
![]() Geometrie Vektoralgebra und analytische Geometrie Vektoralgebra Rechenregeln
Geometrie Vektoralgebra und analytische Geometrie Vektoralgebra Rechenregeln
 der die Diagonale
der die Diagonale 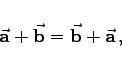

 der den Polygonzug schließt, den die Vektoren
der den Polygonzug schließt, den die Vektoren 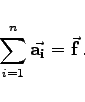
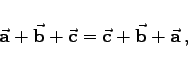


![]() in der linken Abbildung ergibt.
in der linken Abbildung ergibt.