Inhalt Index DeskTop Bronstein
![]()
![]() Geometrie Vektoralgebra und analytische Geometrie Analytische Geometrie der Ebene Hyperbel
Geometrie Vektoralgebra und analytische Geometrie Analytische Geometrie der Ebene Hyperbel
Asymptoten der Hyperbel sind Geraden, die sich den Hyperbelzweigen für ![]() unbegrenzt nähern (s. Definition der Asymptoten).
unbegrenzt nähern (s. Definition der Asymptoten).
Der Richtungskoeffizient der Asymptoten ist ![]() Die Gleichungen der Asymptoten lauten
Die Gleichungen der Asymptoten lauten
 |
(3.357) |
Die Asymptoten bilden gemeinsam mit der Tangente an die Hyperbel in einem Punkt P das Tangentenstück der Hyperbel, d.h. die Strecke ![]() Das Tangentenstück wird durch den Berührungspunkt P halbiert, so daß
Das Tangentenstück wird durch den Berührungspunkt P halbiert, so daß ![]() ist. Der Flächeninhalt des Dreiecks TOT1 zwischen der Tangente und beiden Asymptoten beträgt für jeden Berührungspunkt P
ist. Der Flächeninhalt des Dreiecks TOT1 zwischen der Tangente und beiden Asymptoten beträgt für jeden Berührungspunkt P
 |
(3.358) |
Der Flächeninhalt des Parallelogramms ![]() , das von den Asymptoten und zwei zu ihnen vom Punkt P ausgehenden Parallelen gebildet wird, beträgt
, das von den Asymptoten und zwei zu ihnen vom Punkt P ausgehenden Parallelen gebildet wird, beträgt
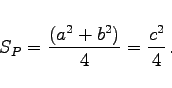 |
(3.359) |