Verkettung von Transformationen

Durch die Kombination verschiedener Grundtransformationen können komplexe geometrische Transformationen realisiert werden.

Es sei eine Folge von Transformationen durch ihre Transformationsmatrizen gegeben. Die Hintereinanderausführung dieser Transformationen überführt den Punkt P(x,y) in n Teilschritten in den Punkt P'. Die resultierende Transformationsmatrix der gesamten Abbildungskette ergibt sich durch Multiplikation der Matrizen:

Entsprechend gilt für die Umkehrung der Transformation

Anstatt also einen Punkt n-mal mittels Grundtransformationen in den Folgezustand zu überführen, kann zunächst die Matrix der Gesamttransformation ermittelt und diese auf den Punkt angewendet werden.
Alle affinen Transformationen lassen sich als Verkettung von Translationen, Rotationen und Skalierungen darstellen. Auch die Verscherung kann als Nacheinanderausführung einer Rotation , einer Skalierung sowie einer weiteren Rotation angegeben werden. Die Parameter , , s_x und s_y können so bestimmt werden, daß gilt.

Beispiel Ermittlung einer Transformationsmatrix

Für eine Rotation um den Winkel um einen beliebigen Punkt Q(x_q,y_q) ergibt sich die Gesamttransformation ergibt sich als Verkettung der folgenden Grundtransformationen:

1. Verschiebung von Q in den Ursprung: .
   
2. Rotation um den Ursprung: .
   
3. Rückverschieben des Ursprungs nach Q:.
   

Die Abfolge der einzelnen Transformationsschritte zeigt folgende Abb. Der Punkt P wird über die Zwischenschritte P₁ und P₂ in den Punkt P' überführt.

Beispiel Spiegelung an einer Geraden

Spiegelung an einer Geraden mit der Geradengleichung y =mx +n:

1. Verschiebung der Geraden, so daß sie durch den Ursprung verläuft: .
2. Rotation der Geraden im Uhrzeigersinn, so daß sie in die x-Achse übergeht: mit .
3. Spiegelung an der x-Achse: .
4. Rückdrehung um : .
5. Umkehrung der Verschiebung, so daß die Gerade wieder an der ursprünglichen Stelle liegt: .

Mit den aus der Trigonometrie bekannten Beziehungen und erhält man die Transformationsmatrix

Beispiel Vollständige und unverzerrte, zentrierte Abbildung

Vollständige und unverzerrte, zentrierte Abbildung eines rechteckigen Bildausschnittes mit den Seitenlängen a und b in einem Ansichtsfenster mit der Breite c und der Höhe d.

Abfolge der Einzeltransformationen:

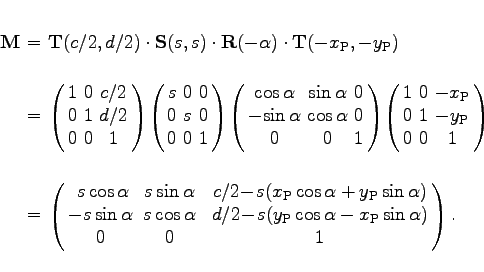1. Verschiebung von in den Ursprung:
   .
2. Rotation um den Winkel im Uhrzeigersinn:
   .
3. Skalierung mit dem Faktor s=s_x=s_y=min(c/a,d/b): .
4. Verschieben des Ursprungs in den Mittelpunkt des Ansichtsfensters: .