Inhalt Index DeskTop Bronstein
![]()
![]() Geometrie Differentialgeometrie Ebene Kurven Lokale Elemente einer Kurve
Geometrie Differentialgeometrie Ebene Kurven Lokale Elemente einer Kurve
Er verläuft durch den betreffenden Kurvenpunkt und hat dort dieselbe 1. und 2. Ableitung wie die Kurve. Demgemäß schmiegt er sich der Kurve im Berührungspunkt besonders gut an. Er wird Schmiegkreis oder Krümmungskreis genannt. Sein Radius heißt Krümmungskreisradius. Es zeigt sich, daß er der Kehrwert des Absolutbetrages der Kurvenkrümmung ist.
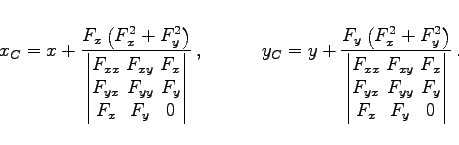 |
(3.522) |
Diese Formeln können auch in der Form
hingeschrieben werden, wobei R gemäß (3.515) bis (3.518) berechnet wird.