Inhalt Index DeskTop Bronstein
![]()
![]() Geometrie Differentialgeometrie Ebene Kurven Evoluten und Evolventen
Geometrie Differentialgeometrie Ebene Kurven Evoluten und Evolventen
Evolute einer gegebenen Kurve heißt eine zweite Kurve, die aus den Krümmungsmittelpunkten der ersten Kurve besteht; sie ist gleichzeitig Einhüllende der Normalen dieser ersten Kurve. Die Einhüllende wird auch Enveloppe genannt. Die Parameterform der Evolute erhält man aus der Gleichung (3.521) für die Krümmungsmittelpunkte, wenn xC und yC als laufende Koordinaten aufgefaßt werden. Wenn es gelingt, aus diesen Gleichungen den Parameter (x, t oder ![]() ) zu eliminieren, dann kann die Evolutengleichung in kartesischen Koordinaten hingeschrieben werden.
) zu eliminieren, dann kann die Evolutengleichung in kartesischen Koordinaten hingeschrieben werden.
| Beispiel |
|
Es ist die Evolute der Parabel y = x2 zu bestimmen.
Aus |
Evolvente oder Involute einer Kurve ![]() heißt eine Kurve
heißt eine Kurve ![]() die für
die für ![]() eine Evolute ist. Daher ist jede Normale PC der Evolvente eine Tangente an die Evolute, und die Bogenlänge
eine Evolute ist. Daher ist jede Normale PC der Evolvente eine Tangente an die Evolute, und die Bogenlänge ![]() der Evolute ist gleich dem Zuwachs des Krümmungsradius der Evolvente (linke Abbildung):
der Evolute ist gleich dem Zuwachs des Krümmungsradius der Evolvente (linke Abbildung):
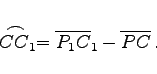 |
(3.537) |
Diese Eigenschaften berechtigen für die Evolvente zu der Bezeichnung Abwickelkurve der Kurve ![]() da sie aus
da sie aus ![]() durch Abwickeln eines gespannten Fadens erhalten werden kann (rechte Abbildung). Einer gegebenen Evolute entspricht eine Schar von Evolventen, die jeweils durch die ursprüngliche Länge des gespannten Fadens bestimmt werden.
durch Abwickeln eines gespannten Fadens erhalten werden kann (rechte Abbildung). Einer gegebenen Evolute entspricht eine Schar von Evolventen, die jeweils durch die ursprüngliche Länge des gespannten Fadens bestimmt werden.
Die Gleichung der Evolute ergibt sich durch Integration eines Systems von Differentialgleichungen, das die Gleichung der Evolute darstellt (s. auch Kreisevolvente).
| Beispiel |
|
Die Katenoide ist die Evolute der Traktrix, die Traktrix die Evolvente der Katenoide. |