Inhalt Index DeskTop Bronstein
![]()
![]() Geometrie Differentialgeometrie Raumkurven Krümmung und Windung
Geometrie Differentialgeometrie Raumkurven Krümmung und Windung
Windung einer Kurve im Punkt P wird eine Zahl genannt, die die Abweichung der Kurve in der unmittelbaren Nähe dieses Punktes von einer ebenen Kurve angibt. Die exakte Definition lautet:
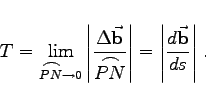 |
(3.553) |
Dabei ist ![]() der Binormalenvektor.
der Binormalenvektor.
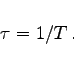 |
(3.554) |
Der Windungsradius ist der Kehrwert der Windung.
wobei die Ableitungen nach s vorzunehmen sind.
wobei ![]() gemäß (3.549) und (3.550) zu berechnen ist.
gemäß (3.549) und (3.550) zu berechnen ist.
Die mit (3.555, 3.556) berechnete Windung kann positiv oder negativ sein. Im Falle T >0 sieht ein Beobachter, der auf der Hauptnormalen parallel zur Binormalen steht, die Windung der Kurve im Rechtsdrehsinn, im Falle T <0 im Linksdrehsinn.
| Beispiel |
|
Die Windung einer Schraubenlinie ist konstant, denn für die Rechtsschraube R bzw. Linksschraube L gilt: |