Inhalt Index DeskTop Bronstein
![]()
![]() Geometrie Differentialgeometrie Flächen Linienelement auf einer Fläche
Geometrie Differentialgeometrie Flächen Linienelement auf einer Fläche
Eine Fläche sei in der Parameterform ![]() (3.563) oder in der Vektorform
(3.563) oder in der Vektorform ![]() bzw.
bzw. ![]() (3.564) gegeben. Auf der Fläche seien P(u,v) ein beliebiger Punkt und N(u + du, v + dv) ein in der Nähe von P liegender zweiter Punkt. Die Länge des Bogens
(3.564) gegeben. Auf der Fläche seien P(u,v) ein beliebiger Punkt und N(u + du, v + dv) ein in der Nähe von P liegender zweiter Punkt. Die Länge des Bogens ![]() auf der Fläche läßt sich dann angenähert durch das Differential des Bogens oder das Linienelement der Fläche mit der Formel
auf der Fläche läßt sich dann angenähert durch das Differential des Bogens oder das Linienelement der Fläche mit der Formel
| E | = |  |
|
| G | = | 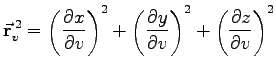 |
(3.575b) |
| Beispiel A | ||
|
Für die Kugel gemäß
|
| Beispiel B | ||
|
Für eine explizit durch z=f(x,y) (3.562) gegebene Fläche ergibt sich:
|