Inhalt Index DeskTop Bronstein
![]()
![]() Geometrie Differentialgeometrie Flächen Krümmung einer Fläche
Geometrie Differentialgeometrie Flächen Krümmung einer Fläche
Zur numerischen Charakterisierung der Krümmung einer Fläche werden hauptsächlich zwei Größen benutzt:
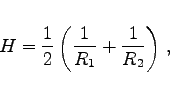 |
(3.587a) |
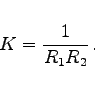 |
(3.587b) |
| Beispiel A |
|
Für den Kreiszylinder mit dem Radius a ist |
| Beispiel B |
|
Für elliptische Punkte ist |
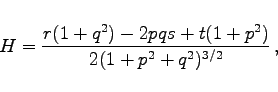 |
(3.588a) |
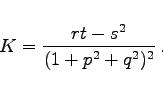 |
(3.588b) |
Die Bedeutung von p, q, r, s, t entspricht (3.584b):
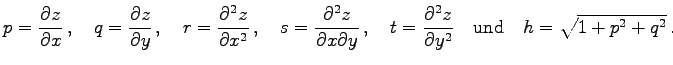
| Beispiel A |
|
|
| Beispiel B |
|
|