Zu einer regulären Matrix 
gibt es immer eine inverse Matrix 
, d.h., die Multiplikation einer Matrix mit ihrer inversen Matrix ergibt immer die Einheitsmatrix:
 |
(4.27a) |
Die Elemente von 
sind
 |
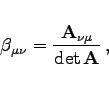(4.27b) |
wobei 
die zum Element 
der Matrix 
gehörende Adjunkte ist. Die praktische Berechnung von 
sollte mit Hilfe von Adjunkten erfolgen. Im Falle einer quadratischen Matrix vom Typ (2,2) gilt:
 |
(4.28) |
Warum in der Matrizenrechnung keine Division von Matrizen eingeführt wurde, sondern mit inversen Matrizen gerechnet wird, hängt damit zusammen, daß die Division nicht eindeutig erklärbar ist. Die Lösungen der Gleichungen
 |
(4.29) |
sind im allgemeinen verschieden.