Inhalt Index DeskTop Bronstein
![]()
![]() Algebra und Diskrete Mathematik Klassische algebraische Strukturen Vektorräume Lineare Operatoren in Vektorräumen
Algebra und Diskrete Mathematik Klassische algebraische Strukturen Vektorräume Lineare Operatoren in Vektorräumen
Es seien V und W zwei Vektorräume. Jede eindeutige Abbildung a von V in W heißt lineare Abbildung, lineare Transformation oder linearer Operator (s. auch Lineare Operatoren und Funktionale) von V in W genau dann, wenn gilt:
 |
(5.231) |
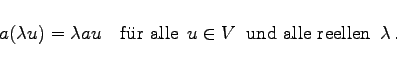 |
(5.232) |
| Beispiel A |
|
Die Abbildung |
Lineare Abbildungen ![]() , bei denen wie in diesem Beispiel
, bei denen wie in diesem Beispiel ![]() gilt, werden lineare Funktionale genannt.
gilt, werden lineare Funktionale genannt.
| Beispiel B |
|
Die Abbildung a des Raumes |
Jedem n-dimensionalen Vektor wird ein Polynom vom Grade ![]() zugeordnet.
zugeordnet.
| Beispiel C |
|
Ist  |