Inhalt Index DeskTop Bronstein
![]()
![]() Algebra und Diskrete Mathematik Mengenlehre Äquivalenz- und Ordnungsrelationen Äquivalenzklassen, Zerlegungen
Algebra und Diskrete Mathematik Mengenlehre Äquivalenz- und Ordnungsrelationen Äquivalenzklassen, Zerlegungen
Jede ─quivalenzrelation R in einer Menge A bewirkt eine Zerlegung Z von A, nńmlich Z =A /R. Umgekehrt bestimmt jede Zerlegung Z einer Menge A eine ─quivalenzrelation R in A:
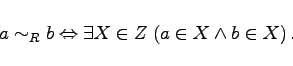 |
(5.91) |
Man kann eine ─quivalenzrelation in einer Menge A als Verallgemeinerung der Gleichheitsbeziehung auffassen, wobei von unwesentlichen Eigenschaften der Elemente von A abstrahiert wird und Elemente, die sich bezŘglich einer gewissen Eigenschaft nicht unterscheiden, zu einer ─quivalenzklasse zusammengefa▀t werden.