Inhalt Index DeskTop Bronstein
Algebra und Diskrete Mathematik Klassische algebraische Strukturen Darstellungen halbeinfacher Lie-Gruppen
Die Darstellung einer halbeinfachen LIE-Algebra in Standardbasis führt im Darstellungsraum Vm auf die m x m-Matrizen 
und 
. Da alle Matrizen 
untereinander kommutieren, können sie gleichzeitig auf Diagonalform gebracht werden; sie besitzen n linear unabhängige, simultane Eigenvektoren 
 |
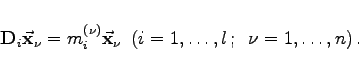(5.157) |
Der Vektor
 |
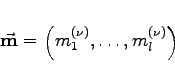(5.158) |
in einem l-dimensionalen Raum wird als Gewicht des Eigenvektors 
bezeichnet. Die Matrixelemente der Diagonalmatrix sind die i-te Komponente der n Gewichtsvektoren 
,
 |
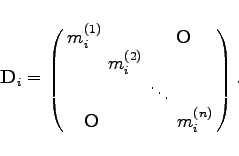(5.159) |
Die Wurzeln 
einer LIE-Algebra und die Gewichte 
ihrer Darstellungen sind in einem Vektorraum gleicher Dimension erklärt. Ein Gewicht heißt einfach, wenn keine Entartung vorliegt. Von zwei Gewichten und 
sagt man ist größer als , wenn in 
die erste von Null verschiedene Komponente positiv ist. Das größte Gewicht einer Darstellung wird auch als höchstes Gewicht bezeichnet. Es gilt: Jede irreduzible Darstellung einer halbeinfachen LIE-Algebra wird durch ihr höchstes Gewicht, das stets einfach ist, eindeutig charakterisiert. Außerdem kann man zeigen: Ist der Vektor 
vom Gewicht , dann ist der Vektor 
vom Gewicht 
:
 |
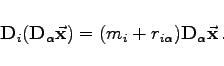(5.160) |
Mit Hilfe der Leiteroperatoren 
lassen sich also -- ausgehend vom Vektor 
zum höchsten Gewicht -- die Eigenvektoren zu allen anderen Gewichten sukzessive konstruieren:
