Inhalt Index DeskTop Bronstein
![]()
![]() Integralrechnung Kurvenintegrale Kurvenintegrale allgemeiner Art
Integralrechnung Kurvenintegrale Kurvenintegrale allgemeiner Art
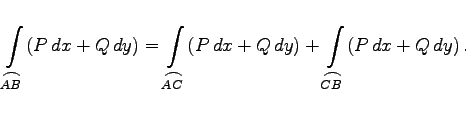 |
(8.119) |
Für den Fall dreier Veränderlicher gelten analoge Formeln.
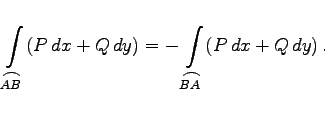 |
(8.120) |
Für den Fall dreier Veränderlicher gelten analoge Formeln.
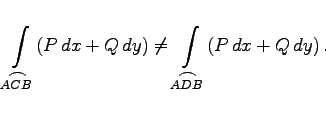 |
(8.121) |
Für den Fall dreier Veränderlicher gelten analoge Formeln.
| Beispiel A |
|
|
| Beispiel B |
|
|